Why are fossil fuels used so widely?
The primary reason is that fossil fuels are cheap and have a high energy density, so the combustion of a certain mass of a fossil fuel generates more energy than can typically be obtained from other energy sources, such as solar panels or wind turbines. Consider the application of energy densities to fuels in a vehicle.

Worked Example
- Most modern vehicles are fueled by gasoline. The energy density of gasoline is about 3.4×104 kJ L-1. Suppose a small car has a fuel tank that can hold 50 L of gasoline: how much energy can be produced from one tank of gasoline?
- Suppose that a new prototype car is able to use solar panels that store the energy needed to operate the vehicle (unfortunately, the storage of solar energy is currently a major technological problem). Assuming that the storage technology is in place, a solar panel with a power capacity of 200 W is able to generate about 1.7×104 kJ of energy per day. If the car is capable of carrying two solar panels, which have stored energy for 6 hours before use, how much energy is obtained? How does this compare to the energy obtained from the combustion of a tank of gasoline?
- How long (in days) would it take the solar panels from part B to generate the same amount of energy that is obtained from the combustion of 50 L of gasoline?
-
Multiply the energy density of gasoline by the volume of the fuel tank.
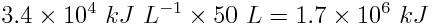
One tank of gasoline generates 1.7×106 kJ, or 1.7 GJ, of energy.
-
First, convert the rate of energy production from a solar panel to energy produced per hour, rather than per day.
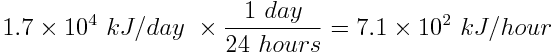
Next, determine how much energy can be stored by one solar panel in 6 hours.
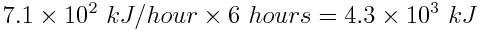
If the car can hold two solar panels, the energy produced in 6 hours is 2×(4.3×103kJ)=8.5×103 kJ. The energy obtained from the combustion of a tank of gasoline (1.7 x 106 kJ) vastly exceeds the energy from two solar panels that store energy for 6 hours. In fact, the energy obtained from the solar panels is only 0.5% of the energy obtained from combustion of 50 L of gasoline.
-
The two solar panels can generate 2×(1.7×104 kJ) =3.4×104 kJ of energy in one day. To find the amount of time for which the panels must store energy to generate the same amount of energy as the combustion of one tank of gasoline, divide the energy generated from the gasoline by the rate of energy production for the two panels.
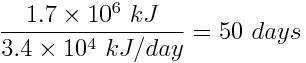
It would take 50 days for the solar panels to store the same amount of energy as was produced by the combustion of one tank of gasoline.